A-OK

Everyone outside the US will be familiar with the standard paper size used in offices around the world, known as A4. You may also be aware that there are other A-series paper sizes, such as the larger A3. Perhaps you have also heard of the B-series sizes.

Have you ever wondered why A4 is the size and shape it is? It may surprise you to learn that there is mathematical beauty in that simple piece of paper you feed into a printer or scribble a note on.

Why a Standard?

It makes a lot of sense to standardise paper sizes; if everyone uses the same paper size, entire industries can be built that provide competition, better pricing, better compatibility, and even less waste. For example, any printer you buy can handle A4 paper. You can buy A4 paper from many different suppliers. The printer you bought 5 years ago likely still works today (assuming it has ink) and uses the same paper sizes it did back then.

The ISO (International Organization for Standardization) standard body actually has a name for international standard paper sizing: ISO 216. This includes the A-series, B-series and C-series paper sizes. This standard is used throughout the world except North America and some parts of Latin America (much like the metric system).

So, if you are going to have a standard, how do you decide the shape of a piece of paper?

Shaping a Standard

Suppose we were creating a new standard for paper. We might decide on some shape purely because we like the look of it. As an example, suppose we decided we wanted to use this random rectangular piece of paper as our standard shape.

We use the space on our page and fill it with a picture of some sort.

Now, as part of our standard we would want smaller (and larger) size pages. It would be great if you could simply halve the page, and use that as a smaller page size. Similarly you could double the page for larger sizes. So let’s halve the page right now, and put our image on this smaller size page.

The problem is, our image now doesn’t fill the entire page (all that blank space is left). If we scale it to fill, our image is stretched and distorted.

What we’d really like is a paper-shape with the property that when you halve it, the new page is the same shape (we say this new page has the same “aspect ratio”). That way you can scale an image up or down without distortion. Our page didn’t work like this – can we find a shape that does?

Let’s take a page of width \(a\) and length \(b\) as shown. If we halve the page, we have a smaller sized page with width \(b/2\) and length \(a\).

The aspect ratio of the larger page is \(\frac{a}{b}\). The aspect ratio of the smaller page is then \(\frac{b/2}{a} = \frac{b}{2a}\). We want these to be equal so we have the following equation we can simplify:

$$\begin{align}
\frac{b}{2a} &= \frac{a}{b}\\
b^{2} &= 2a^{2}\\
b &= \sqrt{2}a, \quad \text{where } a > 0, b > 0\end{align}$$

The result shows that we want the \(length\) of the page to be \(\sqrt{2}\times width\) of the page. If we choose our page size using this ratio, the aspect ratio is preserved as we halve or double the paper size.

Let’s take A4. If you get a ruler and measure an A4 sheet of paper you will find it has a width of \(210 \text{ mm}\) and a height of \(297 \text{ mm}\). From our formula, \(\sqrt{2}\) of the width should give us the length. Let’s calculate the length given that width, using our formula:

$$\begin{align}
length &= \sqrt{2}\times 210\\
&= 1.4142\ldots \times 210\\
&= 296.982\ldots\\
&\approx 297 \text{ mm}
\end{align}$$

So yes, A4 has the right dimensions so that we retain the aspect ratio as we halve or double the page size.

Defining a Series

This \(\sqrt{2}\) factor is called the “Lichtenberg ratio” and was discovered over 200 years ago. Over the years, there was much discussion about paper sizes and utilising this ratio, with a number of standards produced based on this clever bit of mathematics. What we use today finally became an ISO standard in 1975.

The A-series defines paper sizes from A0 through to A10. Larger sizes than A0 were added, and labelled as 2A0 and 4A0, though they are rarely used.

The following shows how these paper sizes are formed by dividing each size in half, starting at A0, going through to A5. You could continue halving to make A6 onwards..

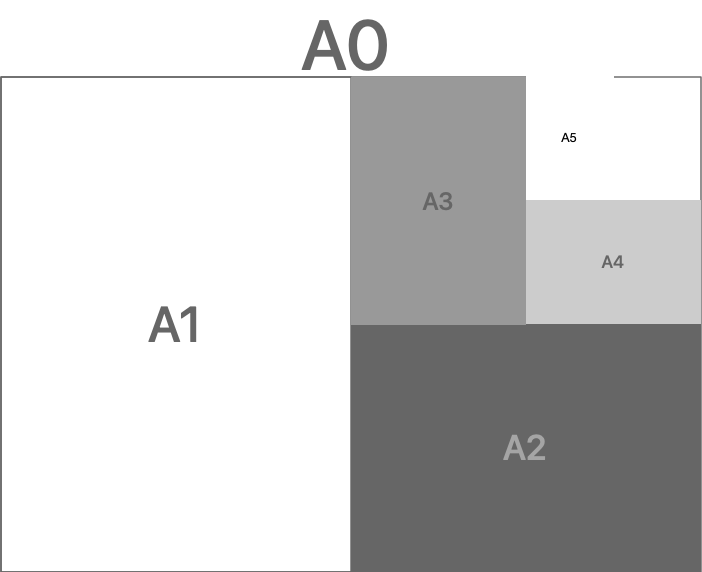
So now we understand why A4 paper is the shape it is, and how it fits into other A-series paper sizes. It’s a great system as you can scale sizes up or down with a constant aspect ratio for that paper. And it is a beautiful application of mathematics.

Choosing a Size

So why is A4 paper the size it is? Who decided it was \(210 \times 297 \text{ mm}\)?

Even here there is beauty in the decision made. Someone could have just chosen the dimensions based on a whim, but instead, the inventors of the standard tied the size back to our wonderful metric system.

It was decided to define A0 as having an area of exactly \(1 \text{ m}^{2}\).

This simple definition adds to the mathematical beauty of the entire standard. In fact, let’s look at what this means and calculate all the sizes of A-series paper (within the limits of whole millimetres).

Let’s say the width of A0 is \(w_{0}\). Then the length \(l_{0}\) is \(\sqrt{2}w_{0}\). We’ll define the area of A0 as \(A_{0}\). Then:

$$\begin{align}
A_{0} &= w_{0} \cdot l_{0}\\
&= w_{0} \cdot \sqrt{2}w_{0}\\
&= \sqrt{2}{w_{0}}^{2}
\end{align}$$

Given \(1 \text{ m}^{2} = 10^6 \text{ mm}^2\) we have:

$$\begin{align}
10^6 &= \sqrt{2}{w_{0}}^{2}\\
{w_{0}}^2 &= \frac{10^6}{\sqrt{2}}\\
w_{0} &= \sqrt{\frac{10^6}{\sqrt{2}}}\\
&= \sqrt{10^6}\sqrt{\frac{1}{\sqrt{2}}}\\
&= 10^{3}\sqrt{\frac{\sqrt{2}}{2}}\\
&= 10^{3}{\left(\frac{\sqrt{2}}{2}\right)}^{\frac{1}{2}}
\end{align}$$

If we look at A1, \(w_{1}\) should be half of \(l_{0}\). Our formula says \(l_{0} = \sqrt{2}w_{0}\), so:

$$\begin{align}
w_{1} &= \frac{1}{2}\sqrt{2}w_{0}\\
&= w_{0}\frac{\sqrt{2}}{2}\\
&= 10^{3}{\left(\frac{\sqrt{2}}{2}\right)}^{\frac{1}{2}} \cdot \frac{\sqrt{2}}{2}\\
&= 10^{3}{\left(\frac{\sqrt{2}}{2}\right)}^{1 + \frac{1}{2}}
\end{align}$$

A pattern begins to form as you look at A2 and so on. The result is we can generalise this formula, so that

$$w_{n} = 10^{3}{\left(\frac{\sqrt{2}}{2}\right)}^{n + \frac{1}{2}}$$

We now have a formula to work out the width of any size in the A-series. And a formula to work out the length given the width.

Let’s write a small Swift script to print out the width and length of A0–A10.

#!/usr/bin/swift
// aseries.swift
// Calculates A-series paper width and length for A0–A10

import Foundation 

func dimensions(_ n: Int) -> (Double, Double) {
    let w = 1000 * pow(sqrt(2.0)/2, Double(n) + 0.5)
    let l = w * sqrt(2.0)
    return (w,l)
}

for n in 0...10 {
    let (w, l) = dimensions(n)
    let sw = String(format: "%3d", Int(round(w)))
    let sl = String(format: "%3d", Int(round(l)))
    print("A\(n):\t\(sw) mm x \(sl) mm")
}

Running this, we get:

% ./aseries.swift
A0:	841 mm x 1189 mm
A1:	595 mm x 841 mm
A2:	420 mm x 595 mm
A3:	297 mm x 420 mm
A4:	210 mm x 297 mm
A5:	149 mm x 210 mm
A6:	105 mm x 149 mm
A7:	 74 mm x 105 mm
A8:	 53 mm x  74 mm
A9:	 37 mm x  53 mm
A10:	 26 mm x  37 mm

There’s our A4 dimensions as discussed earlier, along with other sizes that make up the standard.

Not the Golden Ratio

The golden ratio is another ratio that is often considered to be aesthetically pleasing. It is sometimes confused with the ratio used in standardised paper sizes, but it is not the same ratio; unfortunately the golden ratio does not have the same property of consistent scaling when used in paper sizing. But it too is a beautiful bit of mathematics and perhaps the subject of a future article.

Conclusion

The great mathematician Bertrand Russel once said that “Mathematics, rightly viewed, possesses not only truth, but supreme beauty”. The paper you use every day is such an example — a beautiful application of mathematics that makes our lives just a little easier. Now that you know the story of that humble piece of paper, you may look at it with new respect for its history and elegance.