
For many of us, we are entering the holiday season. Whether you celebrate Christmas or not, we wish you all the best for the holidays and the New Year.
The Christmas tree has its origins in medieval and pagan traditions going back centuries. Today, the tree is, as the name suggests, associated with Christmas. Here in Australia, it is not uncommon for even non-Christians to celebrate Christmas as a festive time to spend with family and friends. You’ll find Christmas trees in houses all over the country. In that tradition, we send you our best wishes and present you with this mathematically, chaos-generated Christmas card based on the traditional Christmas tree. Here it is, running on an iPhone.
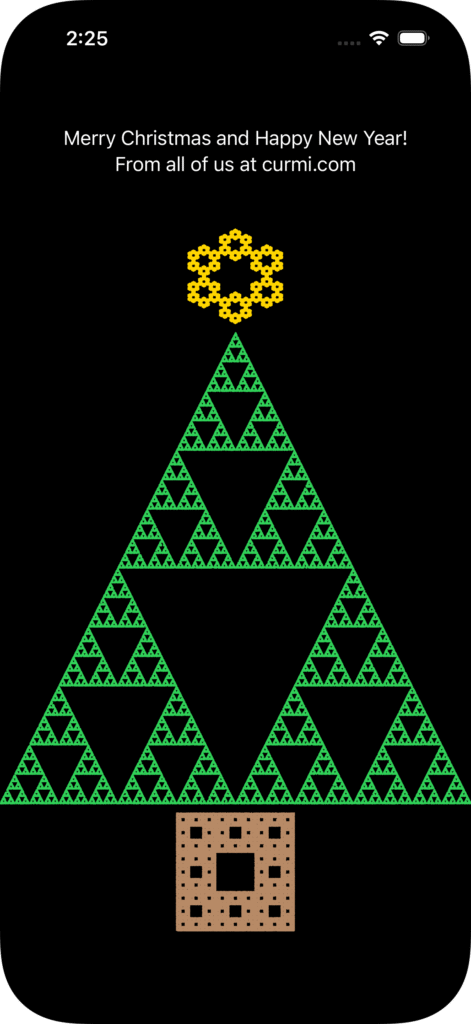
it wouldn’t be curmi.com if there wasn’t some involvement of mathematics and computer science in this simple card, and so the rest of this article will discuss how we generated this card – the mathematics of the fractals, and the full code used to create the shapes.
We know that sometimes maths can appear scary. But why not hang around and check out how these shapes are generated. You may be surprised that the maths is nothing more than basic high school trigonometry, and we’ve simplified all the code to a single file to make it easier to follow, and even try yourself at home.
The Tree
Our Christmas tree consists of 3 basic shapes:
- A Triangle (the tree)
- A Square (the base)
- A Hexagon (the star on top of the tree)
Each shape is actually a fractal. Let’s look at each shape in turn.
The Triangle
Our previous article on Sierpiński Chaos showed us how to generate the triangle that is the basis of our Christmas tree. You should read this article first to understand how this shape is produced, and also the basics of the Chaos Game we used to generate the shape.

The Square
After reading the previous articles on the Sierpiński triangle and how we used the Chaos Game to generate the shape, you may have wondered if a similar game could be played to generate other fractal shapes. And the answer is yes!
For example, if, rather than a triangle, we begin with a square, we can actually generate something called the Sierpiński Carpet.
Similar to the Triangle, the Sierpiński carpet begins with a square. The square is cut into 9 congruent subsquares in a 3-by-3 grid, and the central subsquare is removed. This procedure is then applied recursively to the remaining 8 sub-squares, and so on.
We can use the Chaos Game to generate the Sierpiński carpet. The rules here are very similar to the rules for the Sierpiński triangle, though we also include mid-points of the edges, and we choose a point \(\frac{2}{3}\) along the line from the previous point to the randomly chosen vertex/midpoint.



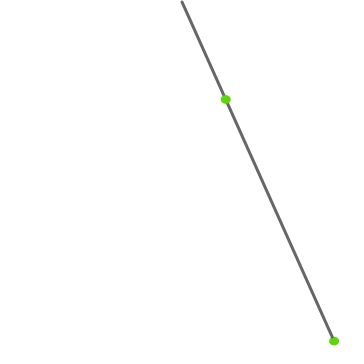
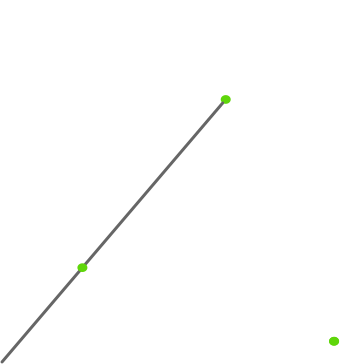
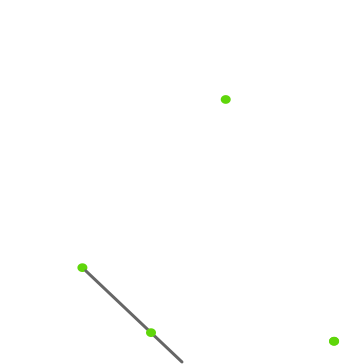
Once again, we don’t want to do this by hand, so we’ll use a computer (an iPhone in this case).
We start with a square, with vertices \(\left(0,0\right)\), \(\left(0,2\right)\), \(\left(2,0\right)\) and \(\left(2,2\right)\). We’ll also find midpoints of the sides, labelled as \(\left(1,0\right)\), \(\left(0,1\right)\), \(\left(1,2\right)\) and \(\left(2,1\right)\). For simplicity we’ll call these mid-points “vertices” (as it makes it easier to reuse the code from the previous article).

Finding a Random Point
In Sierpiński Chaos we mention how starting with a random point along the edge of the shape ensures we don’t have a few points in the wrong spot of our generated shape. We’ll do that for this shape too.
Fortunately, it is easy to find a random point on the edges of a square, as we just randomly choose an edge, and then a random number between \(0\) and \(2\) along the edge. Here’s a simple implementation.
func randomPointOnEdge() -> (Double, Double) {
switch Int.random(in: 0..<4) {
case 0:
return (Double.random(in: 0.0...2.0), 0)
case 1:
return (Double.random(in: 0.0...2.0), 2)
case 2:
return (0, Double.random(in: 0.0...2.0))
default:
return (2, Double.random(in: 0.0...2.0))
}
}
Finding the Next Point
Similar to the triangle, we find the next point by choosing a vertex (in this case, 1 of 8 points), and finding a point \(\frac{2}{3}\) of the way from the previous point to the vertex. If our current point is \(\left(x,y\right)\) and our chosen vertex is \(\left(v,w\right)\), a little bit of maths says this point will be:
\(\left(x+(v-x)\cdot\frac{2}{3}, y+(w-y)\cdot\frac{2}{3}\right)\)
So our code becomes:
let vertices = [(0.0,0.0), (1,0), (2,0), (0, 1), (2,1), (0,2), (1,2), (2,2)]
func randomVertex() -> (Double, Double) {
let index = Int.random(in: 0..<vertices.count)
return vertices[index]
}
func nextPoint(_ x: Double, _ y: Double) -> (Double, Double) {
let (v, w) = randomVertex()
let (a, b) = (x + (v - x) * 2/3, y + (w - y) * 2/3)
return (a, b)
}Generation
Putting the code together using the structure of the previous article generates a Sierpiński Carpet (our square base).

The Hexagon
We can also generate a fractal starting with a hexagon.
The rules will be the same as the square above – that is, we choose a point \(\frac{2}{3}\) along the line from the previous point to a randomly chosen vertex.
We start with a hexagon. We choose the bottom point to be at (1,0).
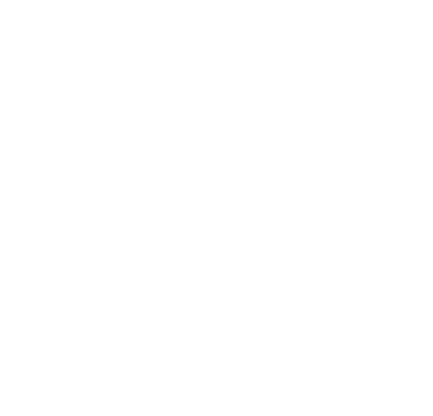
To find all the other vertices, we need a bit of trigonometry. We note that the internal angles of a hexagon are \(120º\), and all sides have the same length \(s\). Let’s look at the bottom left point (\(B\)).
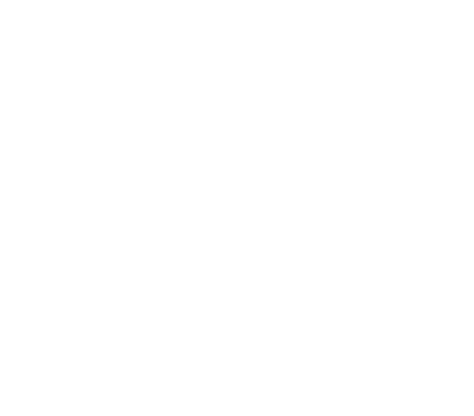
From trigonometry, tan of the angle is the opposite over the adjacent. Also, \(30º\) is \(\frac{\pi}{6}\) in radians, and \(\tan{\frac{\pi}{6}} = \frac{1}{\sqrt{3}}\). This leads to:
$$\begin{eqnarray}\tan{\frac{\pi}{6}} &=& \frac{y}{1}\\y &=& \tan{\frac{\pi}{6}}\\y &=& \frac{1}{\sqrt{3}}\end{eqnarray}$$
Similarly, we can calculate \(s\), given \(\cos{\frac{\pi}{6}} = \frac{\sqrt{3}}{2}\)
$$\begin{eqnarray}\cos{\frac{\pi}{6}} &=& \frac{1}{s}\\s &=& \frac{1}{\cos{\frac{\pi}{6}}}\\s &=& \frac{2}{\sqrt{3}}\end{eqnarray}$$
This gives us \(A\) and \(B\). Calculating other vertices similarly we get:
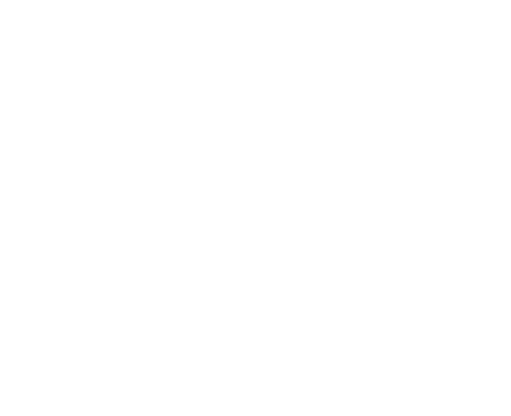
Finding a Random Point
For the vertical edges finding a random point is easy. For the angled edges we need to do some trigonometry, but it is similar to the maths we did for triangle edges in the previous article.
It is left as an exercise for the reader to create the formulas needed, but here’s a simple implementation.
func randomPointOnEdge() -> (Double, Double) {
switch Int.random(in: 0..<6) {
case 0:
return (0, sqrt(3.0)/3 + Double.random(in: 0.0...(2/sqrt(3.0))))
case 1:
let x = Double.random(in: 0.0...1.0)
return (x, sqrt(3.0) + x * sqrt(3.0)/3)
case 2:
let x = Double.random(in: 0.0...1.0)
return (1 + x, sqrt(3.0)*4/3 - x * sqrt(3.0)/3)
case 3:
return (2, sqrt(3.0)/3 + Double.random(in: 0.0...(2/sqrt(3.0))))
case 4:
let x = Double.random(in: 0.0...1.0)
return (1 + x, x * sqrt(3.0)/3)
default:
let x = Double.random(in: 0.0...1.0)
return (x, sqrt(3.0)/3 - x * sqrt(3.0)/3)
}
}
Finding the Next Point
The code for finding the next point is basically the same as the code for the square, with different vertices (and number of vertices).
let vertices = [(1.0,0.0), (0,1/sqrt(3.0)), (0,sqrt(3.0)), (1,4/sqrt(3.0)),
(2,sqrt(3.0)), (2,1/sqrt(3.0))]
func randomVertex() -> (Double, Double) {
let index = Int.random(in: 0..<vertices.count)
return vertices[index]
}
func nextPoint(_ x: Double, _ y: Double) -> (Double, Double) {
let (v, w) = randomVertex()
let (a, b) = (x + (v - x) * 2/3, y + (w - y) * 2/3)
return (a, b)
}Generation
Putting the code together using the structure of the previous article generates the fractal hexagon shape (our star).

Putting It All Together
We now have the 3 shapes that make up our Christmas tree.
We will try and structure the code with some inheritance (we chose to use Swift struct for each shape and inherit from a protocol). We then put these together in our view (with some .containerRelativeFrame use to reduce the size of the star and stand so they don’t take up the full width of the display).
Putting this all together into one Swift program, we have:
import SwiftUI
import Charts
protocol FractalShape {
var vertices: [(Double, Double)] { get }
func randomVertex() -> (Double, Double)
func randomPointOnEdge() -> (Double, Double)
func makeData() -> [(Double, Double)]
func nextPoint(_ x: Double, _ y: Double) -> (Double, Double)
}
extension FractalShape {
func randomVertex() -> (Double, Double) {
let index = Int.random(in: 0..<vertices.count)
return vertices[index]
}
func nextPoint(_ x: Double, _ y: Double) -> (Double, Double) {
let (v, w) = randomVertex()
let (a, b) = (x + (v - x) * 2/3, y + (w - y) * 2/3)
return (a, b)
}
func makeData() -> [(Double, Double)] {
var data:[(Double, Double)] = []
var (x, y) = randomPointOnEdge()
for _ in 0..<100000 {
(x, y) = nextPoint(x, y)
data.append((x, y))
}
return data
}
}
struct FractalTriangle: FractalShape {
var vertices: [(Double, Double)] = [(0,0), (1.0, sqrt(3.0)), (2,0)]
func randomPointOnEdge() -> (Double, Double) {
switch Int.random(in: 0..<3) {
case 0:
return (Double.random(in: 0.0...2.0), 0)
case 1:
let x = Double.random(in: 0.0...1.0)
return (x, x * tan(Double.pi/3))
default:
let x = Double.random(in: 1.0...2.0)
return (x, (2 - x) * tan(Double.pi / 3))
}
}
func nextPoint(_ x: Double, _ y: Double) -> (Double, Double) {
let (v, w) = randomVertex()
let (a, b) = ((x + v) / 2, (y + w) / 2)
return (a, b)
}
}
struct FractalSquare: FractalShape {
var vertices: [(Double, Double)] = [(0.0,0.0), (1,0), (2,0), (0, 1),
(2,1), (0,2), (1,2), (2,2)]
func randomPointOnEdge() -> (Double, Double) {
switch Int.random(in: 0..<4) {
case 0:
return (Double.random(in: 0.0...2.0), 0)
case 1:
return (Double.random(in: 0.0...2.0), 2)
case 2:
return (0, Double.random(in: 0.0...2.0))
default:
return (2, Double.random(in: 0.0...2.0))
}
}
}
struct FractalHexagon: FractalShape {
var vertices: [(Double, Double)] = [(1.0,0.0), (0,1/sqrt(3.0)), (0,sqrt(3.0)),
(1,4/sqrt(3.0)), (2,sqrt(3.0)),
(2,1/sqrt(3.0))]
func randomPointOnEdge() -> (Double, Double) {
switch Int.random(in: 0..<6) {
case 0:
return (0, sqrt(3.0)/3 + Double.random(in: 0.0...(2/sqrt(3.0))))
case 1:
let x = Double.random(in: 0.0...1.0)
return (x, sqrt(3.0) + x * sqrt(3.0)/3)
case 2:
let x = Double.random(in: 0.0...1.0)
return (1 + x, sqrt(3.0)*4/3 - x * sqrt(3.0)/3)
case 3:
return (2, sqrt(3.0)/3 + Double.random(in: 0.0...(2/sqrt(3.0))))
case 4:
let x = Double.random(in: 0.0...1.0)
return (1 + x, x * sqrt(3.0)/3)
default:
let x = Double.random(in: 0.0...1.0)
return (x, sqrt(3.0)/3 - x * sqrt(3.0)/3)
}
}
}
struct ContentView: View {
var body: some View {
Spacer()
Text("Merry Christmas and Happy New Year!")
Text("From all of us at curmi.com")
Spacer()
HStack {
Chart {
let data = FractalHexagon().makeData()
ForEach(0..<data.count, id: \.self) { index in
let (x,y) = data[index]
PointMark(x: .value("x", x), y: .value("y", y))
.symbolSize(1)
.foregroundStyle(.yellow)
}
}
.aspectRatio(1, contentMode: .fit)
.chartXAxis(.hidden)
.chartYAxis(.hidden)
.containerRelativeFrame([.horizontal]) { length, axis in
return length / 5
}
}
Chart {
let data = FractalTriangle().makeData()
ForEach(0..<data.count, id: \.self) { index in
let (x,y) = data[index]
PointMark(x: .value("x", x), y: .value("y", y))
.symbolSize(1)
.foregroundStyle(.green)
}
}
.aspectRatio(1, contentMode: .fit)
.chartXAxis(.hidden)
.chartYAxis(.hidden)
Chart {
let data = FractalSquare().makeData()
ForEach(0..<data.count, id: \.self) { index in
let (x,y) = data[index]
PointMark(x: .value("x", x), y: .value("y", y))
.symbolSize(1)
.foregroundStyle(.brown)
}
}
.aspectRatio(1, contentMode: .fit)
.chartXAxis(.hidden)
.chartYAxis(.hidden)
.containerRelativeFrame([.horizontal]) { length, axis in
return length / 4
}
Spacer()
}
}
#Preview {
ContentView()
}Conclusion
Hopefully that was a fun extension to our look at fractals, with a festive twist. Enjoy your holidays and see you all in the new year.

I look forward to seeing the article where you generate the reindeer!