
The Sierpiński triangle is what is known as a fractal – a geometric shape that shows structure at arbitrarily small scale, often with a similar appearance as the scale changes. The Sierpiński triangle is basically an equilateral triangle, subdivided recursively into smaller equilateral triangles, ad infinitum. It is named after the Polish mathematician Wacław Sierpiński, although the pattern had been used for decoration centuries before but never defined mathematically.

Simple Construction
The triangle can be constructed in a number of ways. As mentioned, the basic approach to creating (and understanding) the triangle is as follows:
- Start with an equilateral triangle.
- Subdivide the triangle into four smaller equilateral triangles of identical shape and size, and remove the central triangle.
- For each of the remaining smaller triangles, repeat step 2.
- Continue this process indefinitely.

However, there is a far more interesting way to construct the Sierpinski triangle.
Chaos
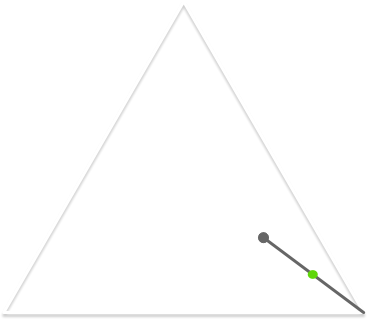
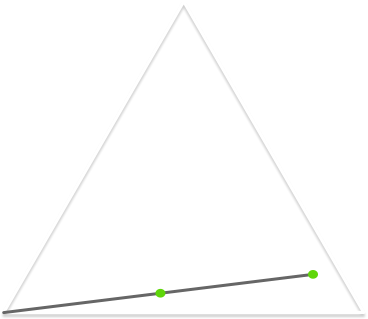
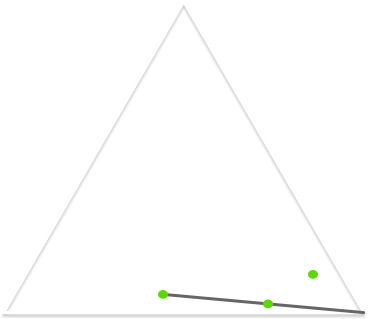
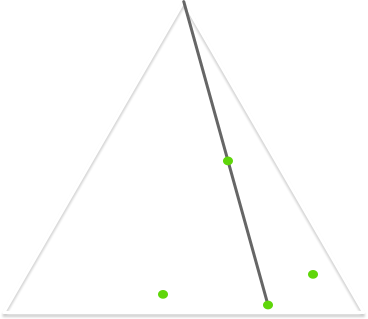
Another way to construct the Sierpiński triangle is via something mathematicians call the Chaos Game. We play the Chaos Game as follows:
- Start with an equilateral triangle.
- Pick a random point inside the triangle as a starting point.
- Chose one of the triangle’s three vertices at random.
- Find the halfway point between your current point and that vertex, and plot a point at that location.
- Use this point as your new starting point, and repeat step 3.
The more points you choose the closer the graph will approximate the Sierpiński triangle. Let’s follow this through visually.


That’s a lot of work to do by hand. Let’s use a computer to do this for us so we can see the result. But before we do that, we need to do some calculations.
Finding a Random Point Inside a Triangle
We want to start with a random point inside our triangle. So how can we do that?
Well, one way would be to find a random point anywhere in a square that contains the triangle, and discard the point and try again if it is outside the triangle. This would work, but it is wasteful (we throw out random points). We can do better. But to do this we need some mathematics.
Let’s start by defining what our initial triangle looks like. We’ll use some actual whole numbers where we can to make this easier on us. So let’s assume the equilateral triangle has side lengths of \(2\) units. Let’s put our origin in the bottom left, making it \(\left(0,0\right)\). And the vertex on the right would be \(\left(2,0\right)\).
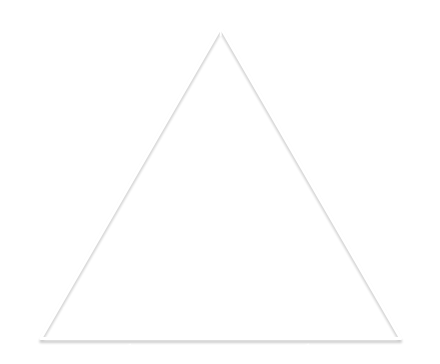
We know the x-coordinate of the top vertex is \(1\), so we need to find \(y\).
Using Pythagoras’s Theorem, we have:
$$\begin{eqnarray}2^2 &=& 1^2 + y^2\\4 &=& 1 + y^2\\{y}^2 &=& 3\\\text{So,} \ y &=& \sqrt{3}\end{eqnarray}$$
So our vertices are \(\left(0,0\right)\), \(\left(2,0\right)\) and \(\left(1,\sqrt{3}\right)\).
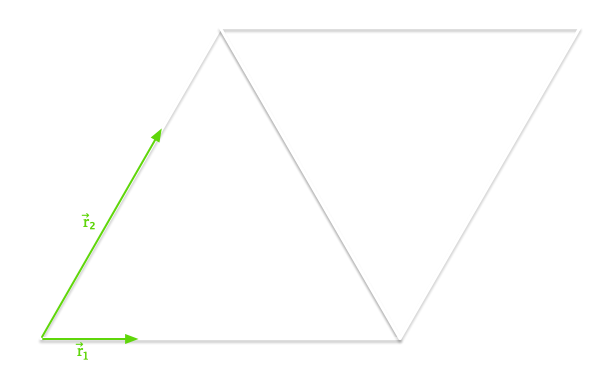
Now, let’s mirror our triangle to form a parallelogram. To find a random point in the parallelogram, we can choose a random point along each of the vertices shown by vectors \(\vec{r_1}\) and \(\vec{r_2}\).
We can add these vectors together (\(\vec{p}\)) to be our random point in the parallelogram.
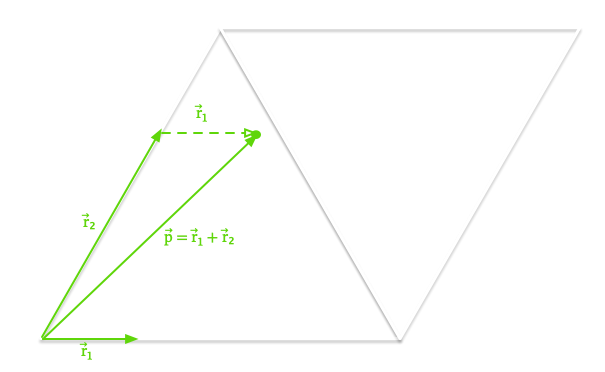
Let \(r_1\) be the magnitude of \(\vec{r_1}\), i.e. \(\lVert \vec{r_1} \rVert\). Similarly \(r_2\) is the magnitude of \(\vec{r_2}\), i.e. \(\lVert \vec{r_2} \rVert\).
If \(r_1 + r_2 > 2\) (the length of a side), \(\vec{p}\) will be in the second triangle part of the parallelogram. We can instead mirror it back to the first with the rule that “if \(r_1 + r_2 > 2\), set \(r_1\) to \(2 – r_1\) and \(r_2\) to \(2 – r_2\)”. This brings the random points back into the first triangle.
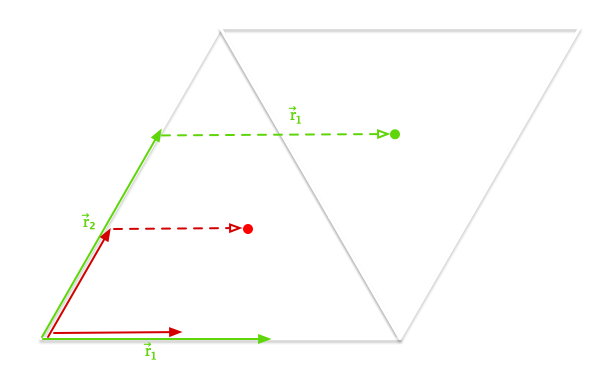
We now have values \(r_1\) and \(r_2\) and can use some trigonometry to convert our vector \(\vec{p}\) to cartesian coordinates \(\left(x,y\right)\).
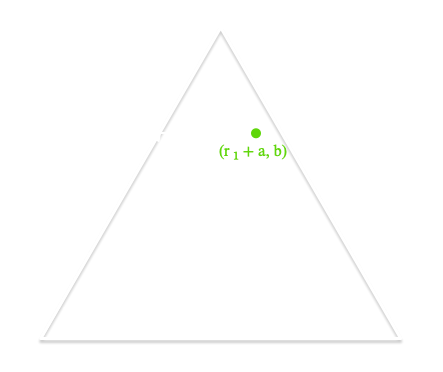
$$\begin{eqnarray}x &=& r_1 + r_2 \cdot \cos{\frac{\pi}{3}}\\y &=& r_2 \cdot \sin{\frac{\pi}{3}}\end{eqnarray}$$
(Recall that \(60^{\circ}\) is \(\frac{\pi}{3}\) in radians.)
We can put that all together into our first bit of code: a function (written in Swift) that returns a random point in our equilateral triangle with side length 2.
func randomPoint() -> (Double, Double) {
var (r1, r2) = (Double.random(in: 0.0...2.0), Double.random(in: 0.0...2.0))
if (r1 + r2) > 2 {
(r1, r2) = (2 - r1, 2 - r2)
}
let (x, y) = (r1 + r2 * cos(Double.pi / 3), r2 * sin(Double.pi / 3))
return (x, y)
}Halfway Point to a Vertex
From any point \(\left(x,y\right)\) to a vertex \(\left(v,w\right)\) we can just add coordinates and divide by \(2\). So the halfway point is:
\(\left(\frac{x+v}{2}, \frac{y+w}{2}\right)\)
Finding a random vertex from the list of three vertices is easy enough, so the code looks something like:
let vertices = [(0,0), (1.0, sqrt(3.0)), (2,0)]
func randomVertex() -> (Double, Double) {
let index = Int.random(in: 0..<3)
return vertices[index]
}
func nextPoint(_ x: Double, _ y: Double) -> (Double, Double) {
let (v, w) = randomVertex()
let (a, b) = ((x + v) / 2, (y + w) / 2)
return (a, b)
}An Application To Demonstrate Construction
Let’s put all that together into an application. Here is my ContentView in a simple SwiftUI application you can compile to run on iOS or macOS. I generate the data points (based on a Picker list of how many random points to generate), and display those points in a SwiftUI Chart.
import SwiftUI
import Charts
struct ContentView: View {
@State var data: [(Double, Double)] = []
@State var num: Int = 10
let vertices = [(0,0), (1.0, sqrt(3.0)), (2,0)]
let choices = [10, 100, 1000, 10000, 100000]
var body: some View {
Picker("", selection: $num) {
ForEach(choices, id: \.self) { n in
Text(verbatim: "\(n)")
}
}
.onChange(of: num) { _, new in
makeData()
}
Spacer()
Chart {
ForEach(0..<data.count, id: \.self) { index in
let (x,y) = data[index]
PointMark(x: .value("x", x), y: .value("y", y))
.symbolSize(1)
.foregroundStyle(.green)
}
}
.aspectRatio(1, contentMode: .fit)
.chartXAxis(.hidden)
.chartYAxis(.hidden)
.onAppear() {
self.makeData()
}
Spacer()
}
func randomPoint() -> (Double, Double) {
var (r1, r2) = (Double.random(in: 0.0...2.0), Double.random(in: 0.0...2.0))
if (r1 + r2) > 2 {
(r1, r2) = (2 - r1, 2 - r2)
}
let (x, y) = (r1 + r2 * cos(Double.pi / 3), r2 * sin(Double.pi / 3))
return (x, y)
}
func randomVertex() -> (Double, Double) {
let index = Int.random(in: 0..<3)
return vertices[index]
}
func nextPoint(_ x: Double, _ y: Double) -> (Double, Double) {
let (v, w) = randomVertex()
let (a, b) = ((x + v) / 2, (y + w) / 2)
return (a, b)
}
func makeData() {
data = []
var (x, y) = randomPoint()
for _ in 0..<num {
(x, y) = nextPoint(x, y)
data.append((x, y))
}
}
}
#Preview {
ContentView()
}Here’s a video of the application running on an iPhone. We can see the form take shape starting at 10 points, then 100, 1000, 10000 and finally 100000 points.
Anomalies
You may have picked up on an issue thinking about the problem, or perhaps you saw it in running the application. It’s possible for some initial points to appear in, what should be, the black areas of the Sierpinski triangle.
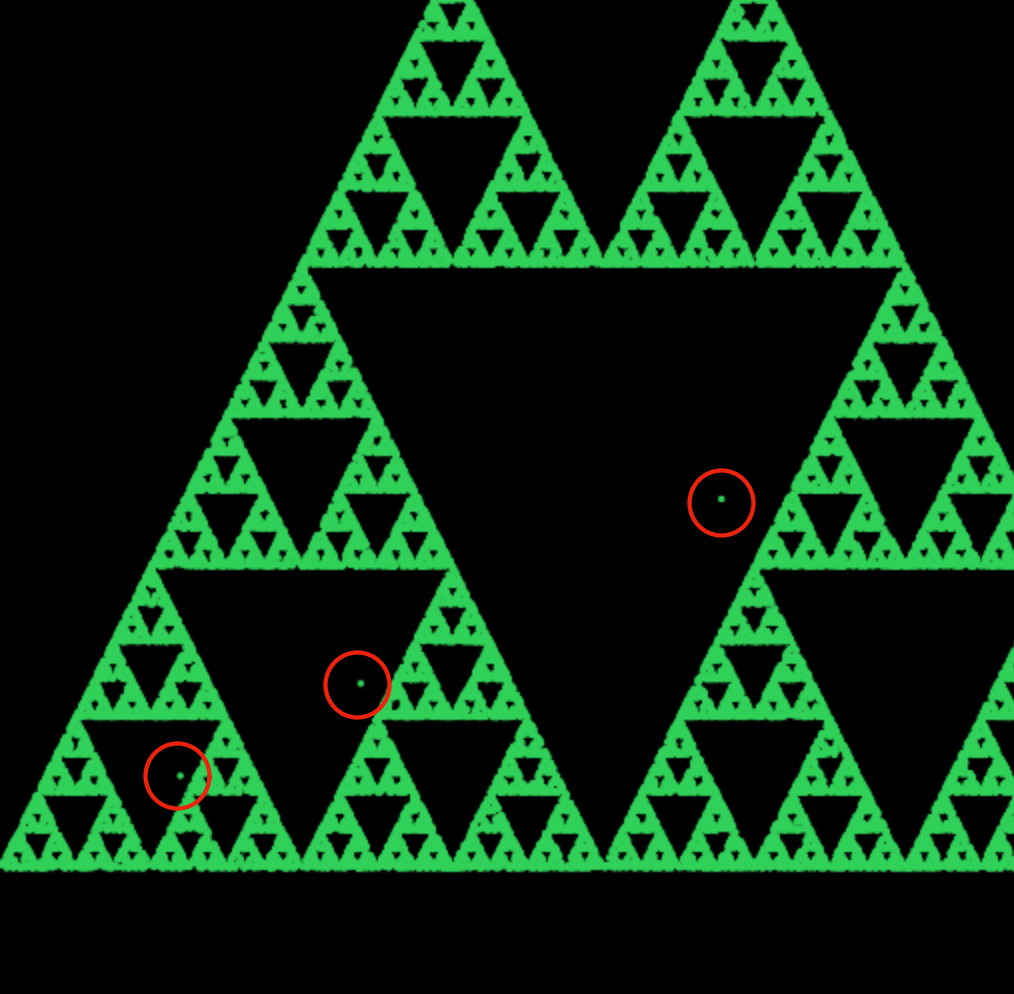
This is because, following the rules of the Chaos Game, we start with any point in the large triangle. It is quite possible for the midpoint from that point to a random vertex to actually be in a black area. Eventually it settles down and creates the triangle as we expect.
One way we can guarantee we get no anomalies is to always start from a random point along the edges of the triangle. We then follow the rules as before, and avoid any points in the black areas.
For completeness, let’s do the maths required here and write a replacement function we could use instead.
For random points along \(\vec{AB}\), define \(x\) as a random value between \(0\) and \(2\). Random points are simply:
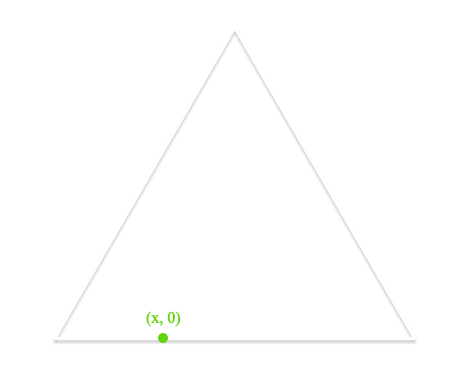
\(\left(x, 0\right)\)
For random points along \(\vec{AC}\), define \(x\) as a random value between \(0\) and \(1\). These will form our x-coordinates. We need to find the y-coordinate on edge \(\vec{AC}\). From trigonometry, random points on \(\vec{AC}\) are therefore:
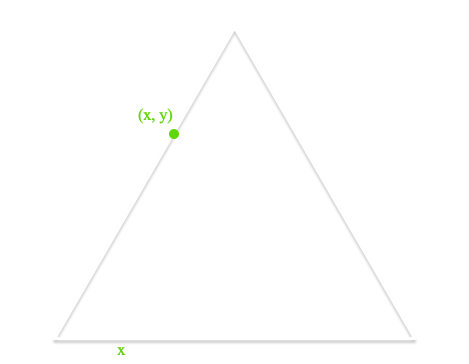
\(\left(x, x \cdot \tan{\frac{\pi}{3}}\right)\)
Similarly, for random points along \(\vec{CB}\), define \(x\) as a random value between \(1\) and \(2\). These will form our x-coordinates. We need to find the y-coordinate on edge \(\vec{CB}\). From trigonometry, random points on \(\vec{AC}\) are therefore:
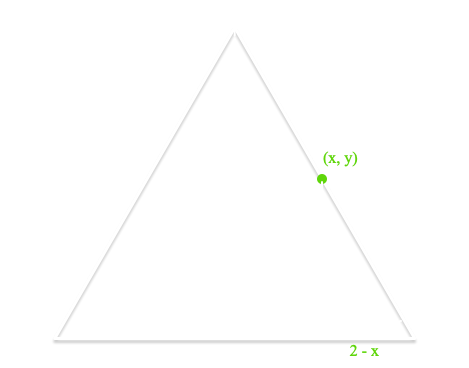
\(\left(x, (2 – x) \cdot \tan{\frac{\pi}{3}}\right)\)
Putting this together into a function we could use, we have:
func randomPointOnEdge() -> (Double, Double) {
switch Int.random(in: 0..<3) {
case 0:
return (Double.random(in: 0.0...2.0), 0)
case 1:
let x = Double.random(in: 0.0...1.0)
return (x, x * tan(Double.pi/3))
default:
let x = Double.random(in: 1.0...2.0)
return (x, (2 - x) * tan(Double.pi / 3)
}
}It’s left as an exercise for the reader to change the code of the main program to use this function.
Conclusion
The Sierpiński triangle has real world applications. For example, the structure has been used in creating multi-band antennas for devices, as the fractal nature allows it to handle multiple frequencies in the one antenna. It has also been used in a new type of authentication system.
Fractals often appear in nature, and the Sierpiński triangle is no exception. Scientists have discovered a microbial enzyme – citrate synthase from a cyanobacterium – that spontaneously assembles into the Sierpinski triangle pattern.
Fractals are also used in video games and movies, creating realistic computer graphics, particularly special effects.
The Sierpinski triangle may not be as famous a fractal as, say, the Mandelbrot set, but it still is a fascinating structure with some practical applications. And hopefully it made for an interesting look at using chaos to generate symmetry.

Excellent work Jamie!